


Complex numbers are written in exponential form . The multiplications, divisions and power of complex numbers in exponential form are explained through examples and reinforced through questions with detailed solutions.
A complex number in standard form \( z = a + ib \) is written in polar form as \[ z = r (\cos(\theta)+ i \sin(\theta)) \] where \( r = \sqrt \) is called the modulus of \( z \) and \( \tan (\theta) = \left (\dfrac \right) \) , such that \( 0 \le \theta \lt 2\pi \) , \( \theta\) is called argument Examples and questions with solutions. of \( z \)
The graphical interpretations of \( a \) , \( b \) , \( r \) and \( \theta \) are shown below for a complex number on a complex plane.
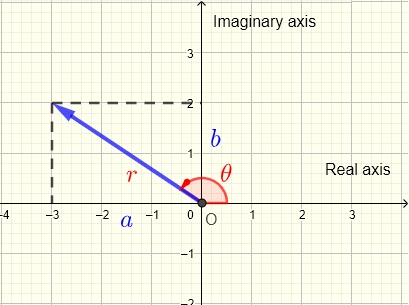


We now use Euler's formula given by \( \displaystyle e^ = \cos \theta + i \sin \theta \) to write the complex number \( z \) in exponential form as follows: \[ z = r e^\] where \( r \) and \( \theta \) as defined above.
Example 1
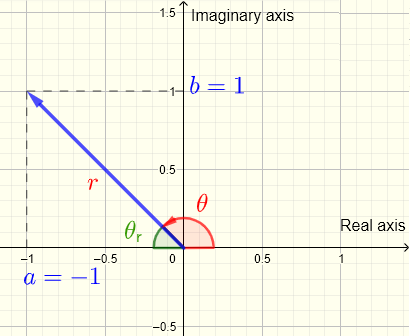
Plot the complex number \( z = -1 + i \) on the complex plane and write it in exponential form .
Solution to Example 1
The complex number \(z = -1 + i = a + i b \) with \( a = -1 \) being the real part and \( b = 1 \) being the imaginary part, is plotted as a vector on a complex plane shown below. It is a vector whose components are the real part \( a \) along the "real axis" and the imaginary part \( b \) along the "imaginary axis". The argument angle \( \theta \) is the angle in counterclockwise direction with initial side starting from the positive real part axis. The modulus \( r = \sqrt = \sqrt = \sqrt 2\) is the length of the vector.


Example 2
a) Plot the complex numbers : \( i , - 2 , - i , - 1 - 2i \) and \( 1 - i \) on the same complex plane.
b) Plot in separate complex planes and write the complex numbers : \( i , - 2 , - i , - 1 - 2i \) and \( 1 - i \) in exponential form .
Solution to Example 2
a) The plot all given complex numbers in the same complex plane is shown below.



b) Plot and write in exponential forms .
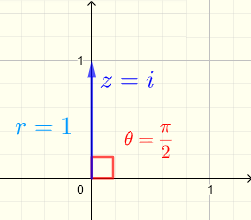
Let \( z = i = a + i b \)
gives \( a = 0 \) and \( b = 1 \)
\( r = \sqrt = 1 \)
\( \tan \theta = \dfrac = undefined \)
An angle whose tangent is undefined is an angle with terminal side on the imaginary axis.
In fact it is easier to determine \( \theta = \dfrac<\pi> \) from the plot of \( z = i \) shown below.
Write in exponential form : \( \quad z = i = r e^ = e^
Let \( z = -2 = a + i b \)
gives \( a = -2 \) and \( b = 0 \)
\( r = \sqrt = 2 \)
\( \tan \theta = \dfrac = 0 \)
An angle whose tangent is equal to 0 is an angle with terminal side on the real axis.
It is easier to determine \( \theta = \pi \) from the plot of \( z = -2 \) shown below.
Write in exponential form : \( \quad z = -2 = r e^ = 2 e^



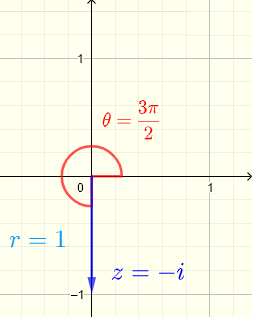
Let \( z = - i = a + i b \)
gives \( a = 0 \) and \( b = - 1 \)
\( r = \sqrt = 1 \)
\( \tan \theta = \dfrac = undefined \)
An angle whose tangent is undefined is an angle with terminal side on the imaginary axis.
We determine \( \theta = \dfrac<3\pi> \) from the plot of \( z = - i \) shown below.
Write in exponential form : \( \quad z = - i = r e^ = e^ < i 3\pi/2>\)


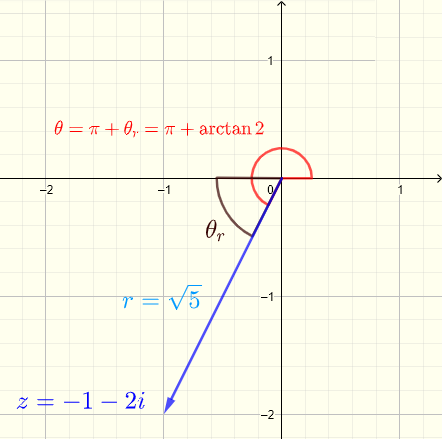
Let \( z = - 1 -2i = a + i b \)
gives \( a = -1 \) and \( b = - 2 \)
\( r = \sqrt = \sqrt 5 \)
First find reference angle: \( \tan \theta_r = |\dfrac| = 2 \) , \( \theta_r = \arctan 2 \)
\( \theta = \pi + \arctan 2 \approx 4.25\)
Write in exponential form : \( \quad z = - 1 -2i = r e^ = \sqrt 5 e^ \)


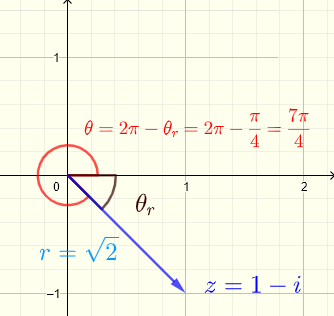
Let \( z = 1 - i = a + i b \)
gives \( a = 1 \) and \( b = - 1 \)
\( r = \sqrt = \sqrt 2 \)
First find reference angle: \( \tan \theta_r = |\dfrac| = 1 \) , \( \theta_r = \dfrac<\pi> \)
\( \theta = 2\pi - \theta_r = 2\pi - \dfrac<\pi> = \dfrac<7\pi> \)
Write in exponential form : \( \quad z = 1 - i = r e^ = \sqrt 2 e^ \)


Example 3
Write complex number \( z = \sqrt2 e^< i \dfrac<5\pi>> \) in standard form.
Solution to Example 3
\( z = \sqrt2 e^< i \dfrac<5\pi>> \)
Use Euler's formula
\( = \sqrt2(\cos(\dfrac<5\pi>)+ i \sin(\dfrac<5\pi>)) \)
Simplify
\( = \sqrt2(-\dfrac - i \dfrac) \)
\( = - 1 - i \)
Complex numbers in exponential form are easily multiplied and divided. The power and root of complex numbers in exponential form are also easily computed
Let \( z_1 = r_1 e^ < i \theta_1>\) and \( z_2 = r_2 e^ < i \theta_2>\) be complex numbers in exponential form .
The product of \( z_1 \) and \( z_2 \) is given by
\[ z_1 z_2 = r_1 r_2 e ^ < i (\theta_1+\theta_2) >\]
Example 3
Given \( z_1 = 3 e^ < i \pi/4 >\) and \( z_2 = 5 e^ \)
Find \( z_1 z_2\) and write it in standard form.
Solution to Example 3
\( z_1 z_2 = (3 e^< i \pi/4 >) (5 e^ < i 3 \pi/4 >)\)
Multiply the modulii \( 3 \) and \( 5 \) together and apply exponent rule apply the rule of exponents \( e^x e^y = e^ \)
\( = (3 \times 5) e^ < i\pi/4 + i 3\pi/4 >\)
Simplify
\( = 15 e^ < i \pi >\)
Rewrite in polar form
\( = 15 (\cos \pi + i \sin \pi) \)
Simplify
\( = - 15 \)
Let \( z_1 = r_1 e^ < i \theta_1>\) and \( z_2 = r_2 e^ < i \theta_2 >\) be complex numbers in exponential form .
The ratio (or division) of \( z_1 \) and \( z_2 \) is given by
\[ \dfrac < z_2>= \dfrac e ^ < i (\theta_1-\theta_2) >\]
Example 4
Given \( z_1 = 10 e^ < i \pi/3 >\) and \( z_2 = 2 e^ < i 2\pi/3 >\)
Find the product \( \dfrac \) and write it in standard form.
Solution to Example 4
\( \dfrac = \dfrac> >\)
Divide the modulii \( 10 \) by \( 2 \) and apply the rule of exponents \( \dfrac = e^ \)
\( = \dfrac e^ < i ( \pi/3 - 2\pi/3 ) >\)
\( = 5 e^ < - i \pi/3 >\)
Rewrite in polar form
\( = 5 (\cos (- \pi/3) + i \sin (- \pi/3) ) \)
Simplify
\( = 5(1/2 - \dfrac i) = \dfrac - \dfrac i \)